These are the low level functions where the actual FFT is performed. Both slow and fast implementations are available for historical reasons. They have identical functionality. At this time, vectors of complex numbers are handled as pairs of vectors of real and imaginary numbers.
What is a Fourier Transform ?
The Fourier transform of a signal gives us a frequency-domain representation of a time-domain signal. In discrete time, the Fourier Transform is called a Discrete Fourier Transform (DFT) and is given by:
![\[y_k = \sum_{t=0}^{n-1} x_t \; \omega_{n}^{kt} \; ; \; k=0...n-1 \]](form_28.png)
where 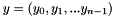 is the DFT (of order
is the DFT (of order 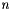 ) of the signal
) of the signal 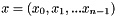 , where
, where 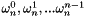 are the n complex nth roots of 1.
are the n complex nth roots of 1.
The Fast Fourier Transform (FFT) is a very efficient implementation of a Discrete Fourier Transform. See, for example "Algorithms" by Thomas H. Cormen, Charles E. Leiserson and Ronald L. Rivest (pub. MIT Press), or any signal processing textbook.
Basic in-place FFT.
There's no point actually using this - use fastFFT instead. However, the code in this function closely matches the classic FORTRAN version given in many text books, so is at least easy to follow for new users.
The length of real and imag must be the same, and must be a power of 2 (e.g. 128).
- See also
- slowIFFT
-
FastFFT
Definition at line 173 of file fft.cc.
Alternate name for slowFFT.
Definition at line 91 of file EST_fft.h.
Basic inverse in-place FFT.
Definition at line 179 of file fft.cc.
Alternate name for slowIFFT.
Definition at line 101 of file EST_fft.h.
Power spectrum using the fastFFT function.
The power spectrum is simply the squared magnitude of the FFT. The result real and imaginary parts are both set equal to the power spectrum (you only need one of them!)
Definition at line 222 of file fft.cc.
Power spectrum using the slowFFT function.
Definition at line 209 of file fft.cc.
Fast FFT An optimised implementation by Tony Robinson to be used in preference to slowFFT.
Definition at line 256 of file fft.cc.

![\[y_k = \sum_{t=0}^{n-1} x_t \; \omega_{n}^{kt} \; ; \; k=0...n-1 \]](form_28.png)
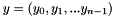 is the DFT (of order
is the DFT (of order 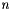 ) of the signal
) of the signal 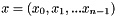 , where
, where 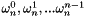 are the n complex nth roots of 1.
are the n complex nth roots of 1.