 |
Edinburgh Speech Tools
2.1-release
|
|
|
Edinburgh Speech Tools
2.1-release
|
|
Signal processing examples
A number of types of signal processing can be performed by the sig2coef function. The following code demonstrates a simple case of calculating the linear prediction (LP) coefficients for a waveform.
First set the order of the lpc analysis to 16 (this entails 17 actual coefficients) and then load in the waveform to be analysed.
Now allocate enough space in the track to hold the analysis. The following command resizes fv to have enough frames for analysis frames at 0.01 intervals up to the end of the waveform, (sig.end()), and enough channels to store lpc_order + 1 coefficients. The channels are named so as to take lpc coefficients.
The positions of the frames, corresponding to the middle of their analysis window also need to be set. For fixed frame analysis, this can be done with the EST_Track::fill_time() function:
The simplest way to do the actual analysis is as follows, which will fill the track with the values from the LP analysis using the default processing controls.
In this style of analysis, default values are used to control the windowing mechanisms which split the whole signal into frames.
Specifically, each frame is defined to start a certain distance before the time interval, and extending the same distance after. This distance is calculated as a function of the local window spacing and can be adjusted as follows:
Extending one time period before and one time period after the current time mark:
Extending 1.5 time periods before and after the current time mark, etc;
The type of windowing function may be changed also as this can be passed in as an optional argument. First we create a window function (This is explained more in Windowing).
and then pass it in as the last argumentMost of the core signal processing functions operate on individual frames of speech and are oblivious as to how these frames were extracted from the original speech. This allows us to take the frames from anywhere in the signal: specifically, this facilitates two common forms of analysis:
It is a simple matter to fill the time array, but normally pitchmarks are read from a file or taken from another signal processing algorithm (see "Pitchmark functions").
There are many ways to fill the time array for fixed frame analysis.
manually:
or by use of the member function EST_Track::fill_time
Pitch synchronous values can simply be read from pitchmark files:
Regardless of how the time points where obtain, the analysis function call is just the same:
Multiple types of feature vector can be stored in the same Track. Imagine that we want lpc, cepstrum and power coefficients in that order in a track. This can be achieved by using the sig2coef function multiple times, or by the wrap around sigpr_base function.
It is vitally important here to ensure that before passing the track to the signal processing functions that it has the correct number of channels and that these are appropriately named. This is most easily done using the track map facility, explained in Naming Channels.
For each call, we only us the part of track that is relevant. The EST_Track::sub_track member function is used to get this. In the following example, we are assuming here that fv has sufficient space for 17 lpc coefficients, 8 cepstrum coefficients and power and that they are stored in that order.
An alternative is to use add_channels_to_map() which takes a list of coefficient types and makes a map. The order of each type of processing is extracted from op.
After allocating the right number of frames and channels in fv, we extract a sub_track, which has all the frames (i.e. between 0 and EST_ALL) and all the lpc channels.
now call the signal processing function on this part:
We repeat the procedure for the cepstral coefficients, but this time take the next 8 channels (17-24 inclusive) and calculate the coefficients:
Extract the last channel for power and call the power function:
While the above technique is adequate for our needs and is a useful demonstration of sub_track extraction, the sigpr_base function is normally easier to use as it does all the sub track extraction itself. To perform the lpc, cepstrum and power analysis, we put these names into a EST_StrList and call sigpr_base.
This will call sigpr_track as many times as is necessary.
Delta coefficients represent the numerical differentiation of a track, and acceleration coefficients represent the second order numerical differentiation.
By convention, delta coefficients have a "_d" suffix and acceleration coefficients "_a". If the coefficient is multi-dimensional, the numbers go after the "_d" or "_a".
Given a EST_Track of coefficients fv, the EST_Track::delta function is used to produce the delta equivalents del. The following uses the track allocated above and generates a set of cepstral coefficients and then makes their delta and acc:
It is possible to directly calculate the delta coefficients of a type of coefficient, even if we don't have the base type. sigpr_delta will process the waveform, make a temporary track of the required type "lpc" and calculate the delta of this.
The following makes a set of delta reflection coefficients:
an equivalent function exists for acceleration coefficients:
The EST_Window class provides a variety of means to divide speech into frames using windowing mechanisms.
A window function can be created from a window name using the EST_Window::creator function:
This function can then be used to create a EST_TBuffer of window values. In the following example the values from a 256 point hamming window are stored in the buffer win_vals:
The make_window function also creates a window:
this can then be used to make a frame of speech from the main EST_Wave sig. The following example extracts speech starting at sample 1000:
Alternatively, exactly the same operation can be performed in a single step by passing the window function to the EST_Window::window_signal function which takes a EST_Wave and performs windowing on a section of it, storing the output in the EST_FVector frame.
The window function need not be explicitly created, the window signal can work on just the name of the window type:
The signal processing library provides an extensive set of functions which operate on a single frame of coefficients. The following example shows one method of splitting the signal into frames and calling a signal processing algorithm.
First set up the track for 16 order LP analysis:
In this example, we take the analysis frame length to be 256 samples long, and the shift in samples is just the shift in seconds times the sampling frequency.
Now we set up a loop which calculates the frames one at a time. start is the start position in samples of each frame. The EST_Window::window_signal function is called which makes a EST_FVector frame of the speech via a hamming window.
Using the EST_Track::frame function, the EST_FVector coefs is set to frame k in the track. It is important to understand that this operation involves setting an internal smart pointer in coefs to the memory of frame k. This allows the signal processing function sig2lpc to operate on an input and output EST_FVector, without any copying to or from the main track. After the sig2lpc call, the kth frame of fv is now filled with the LP coefficients.
A slightly different tack can be taken for pitch-synchronous analysis. Setting up fv with the pitchmarks and channels:
Set up as before, but this time calculate the window starts and lengths from the time points. In this example, the length is a factor (twice) the local frame shift. Note that the only difference between this function and the fixed frame one is in the calculation of the start and end points - the
windowing, frame extraction and call to sig2lpc are exactly the same.
In the EST library we so far have two main types of filter, finite impulse response (FIR)** filters and linear prediction (LP) filters. infinite impulse response (IIR) filters are not yet implemented, though LP filters are a special case of these.
Filtering involves 2 stages: the design of the filter and the use of this filter on the waveform.
First we examine a simple low-pass filter which attempts to suppress all frequencies about a cut-off. Imagine we want to low pass filter a signal at 400Hz. First we design the filter:
And now use this filter on the signal:
For one-off filtering operations, the filter design can be done in the filter function itself. The FIRlowpass_filter function takes the signal, cut-off frequency and order as arguments and designs the filter on the fly. Because of the overhead of filter design, this function is expensive and should only be used for one-off operations.
The equivalent operations exist for high-pass filtering:
Filters of arbitrary frequency response can also be designed using the design_FIR_filter function. This function takes a EST_FVector of order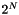 
which specifies the desired frequency response up to 1/2 the sampling frequency. The function returns a set of filter coefficients that attempt to match the desired reponse.
The normal filtering functions can cause a time delay in the filtered waveform. To attempt to eliminate this, a set of double filter function functions are provided which guarantees zero phase differences between the original and filtered waveform.
Sometimes it is undesirable to have the input signal overwritten. For these cases, a set of parallel functions exist which take a input waveform for reading and a output waveform for writing to.
1.8.11